벡터란 무엇인가?
- 크기와 방향을 같이 갖는 양을 표현하는 것을 벡터라 한다.
크기만 표현한 것은 스칼라 라고 한다.
단위벡터
- 벡터의 크기가 1인 경우를 단위 벡터라 한다.
단위 벡터는 방향을 나타내는데 조금 더 집중하고 있다라고 이해하면 된다.
0벡터
- 크기가 0인 벡터, 방향은 고려하지 않는다.
ex) |AA ->| = 0
위치벡터
- 시점이 통일된 벡터
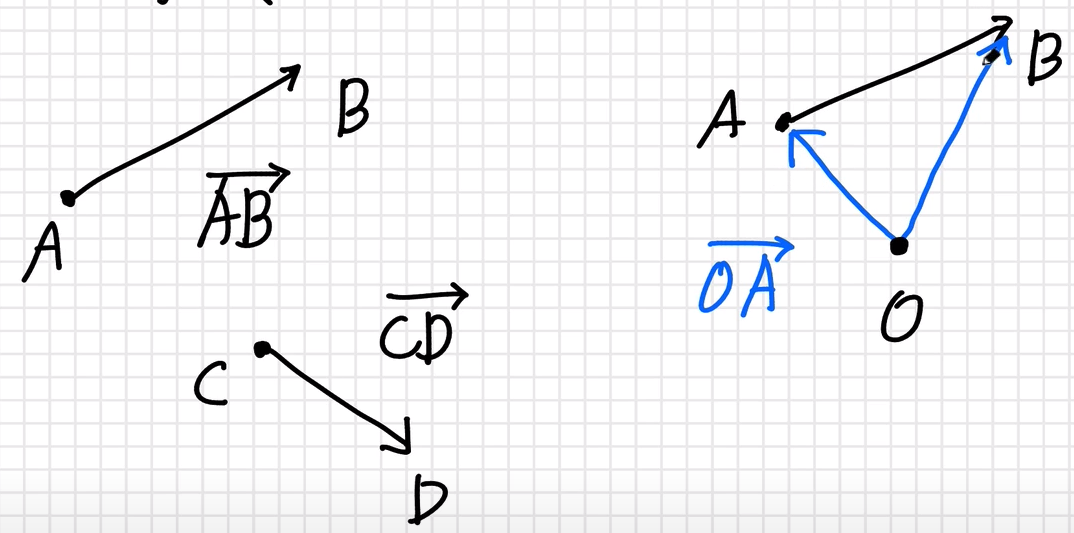
평면 벡터의 성분

시점을 좌표의 0점으로 두고 벡터를 좌표를 표현하듯이 표현하는 것을 성분 벡터라 한다.
성분으로 표현하면 벡터들의 덧셈 뺄셈 실수배가 쉬워진다.

벡터의 길이(스칼라)
- 벡터는 크기와 방향을 갖고, 스칼라는 오직 크기만 갖는다.
이 말은 회전변환(바라보는 관점, 혹은 시작점이 변하면)하면 벡터는 변하고, 스칼라는 변하지 않는다.
예를 들어 서울에서 부산까지 시속 300km로 간다고 했을때,
300km라는 속력은 변하지 않지만
서울 -> 부산으로 갈때와 부산 -> 서울로 갈때는 방향이 변한다. 속도가 달라진다.
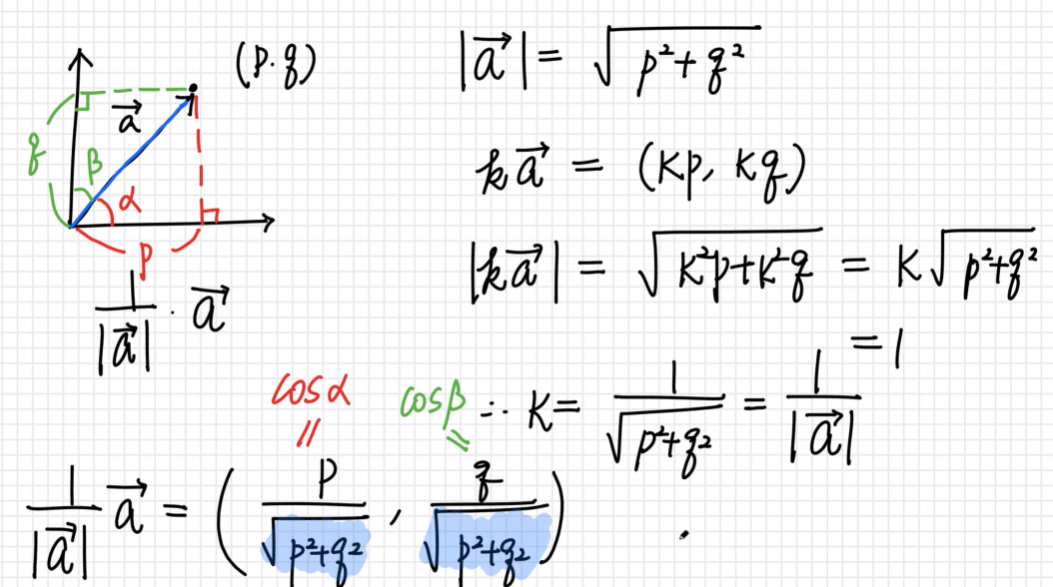
벡터의 정규화
- 벡터의 크기를 1로 만드는 것을 벡터의 정규화(normalize) 라고 한다.
방향만 원할때 사용한다. (방향 벡터)

벡터의 합연산

a-> 와 b->를 합한다고 한다면, a->만큼 이동한 거리에서 b->만큼 이동한 거리에 가상의 선을 그으면 된다.
벡터의 곱연산
벡터의 곱셈은 두가지가 있다. 곱해서 스칼라(실수)가 되는 내적과 곱해서 벡터가 되는 외적이 있다.
내적
내적의 곱은 ㆍ으로 표현한다.
내적의 정의는 벡터a의 크기 * 벡터b의 크기 * 코사인(두 벡터 사이의 각) 이다.
내적의 기하학적 의미는 한 벡터(a)를 다른 벡터(b) 위로 정사영 시킨 길이와 다른벡터(b)의 길이의 곱이라고 볼 수 있다.


외적
a벡터와 b벡터에 동시에 수직인 벡터
외적의 성분


외적 공식
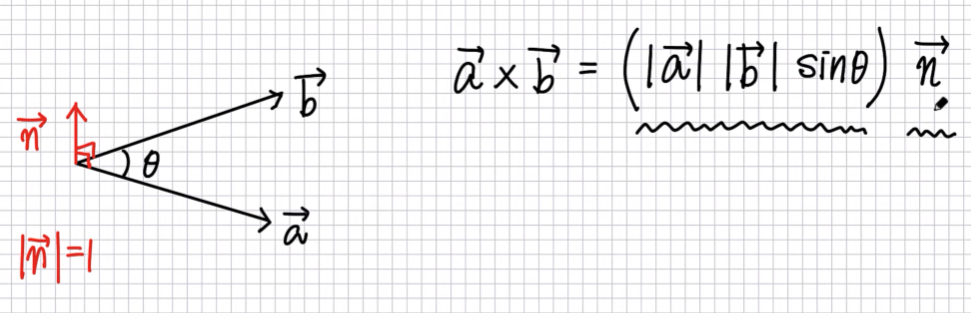
'게임개발 수업' 카테고리의 다른 글
| STL Deque & STL Map (0) | 2023.01.16 |
|---|---|
| 행렬 (0) | 2022.12.15 |
| 비트연산과 쉬프트연산 (0) | 2022.12.13 |
| 삼각비, 삼각함수 (0) | 2022.12.07 |
| WINAPI (0) | 2022.12.05 |


